Measuring Distance with Pythagoras

A common task in computer games is measuring distance. We must know if two objects are close together or far apart. For example, if a big spiky ball is close to a delicate bloon, the bloon might pop!

Good news. It's very easy to measure distance, using just a couple of easy-to-measure numbers. All you need is the Pythagorean Theorem.

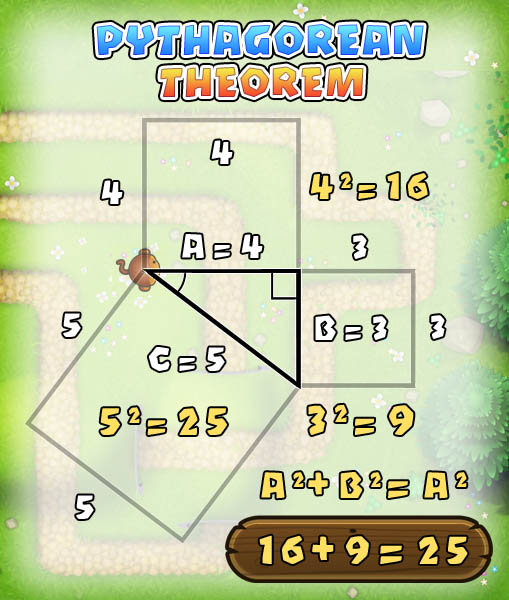
The Theorem states that the square of the hypotenuse in a right-angle triangle is equal to the square of the other two sides, or more succinctly:

A^2 + B^2 = C^2

We're not interested in knowing squares, so we can rearrange:

C = sqrt( A^2 + B^2 )

And that's the version we'll use to find the hypotenuse.

Measuring Distance Between Two Points

We can use Pythagoras to measure distances. All we need to know are the distances in X and Y. We can use those distances as sides A and B of a right-angle triangle. Thus the hypotenuse or length is the square root of X^2 + Y^2.

This is going to come in super handy.