Step 4: Using Sine and Cosine to determine the velocities

We know the player can face any direction in 360 degrees, but what x velocity and what y velocity should we give the player to make it move in the right direction?

If we want the player to have a velocity of 200, then we can visualize our velocity as a line that points in that direction. Currently 200 x velocity only works if the player is facing to the right, with the velocity line along the x axis.

But if we want our velocity to go in the same direction that the player is facing, then that line will rotate around with the player.

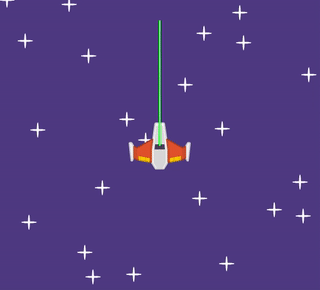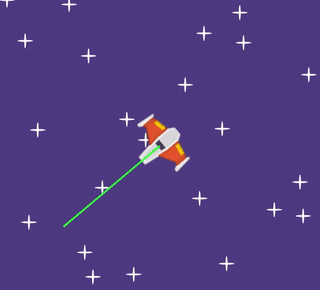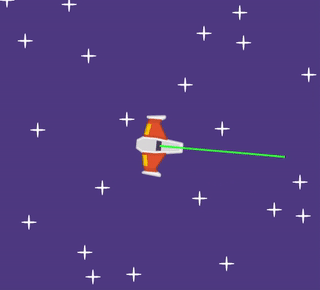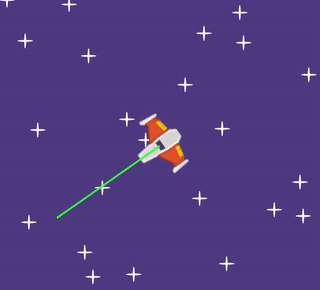
We want this directional velocity to be 200. As the line turns away from the x axis (horizontal), the x velocity shrinks, and the y velocity grows.

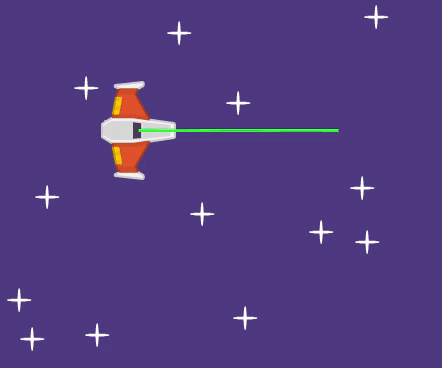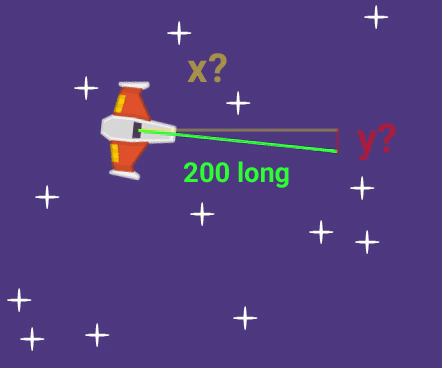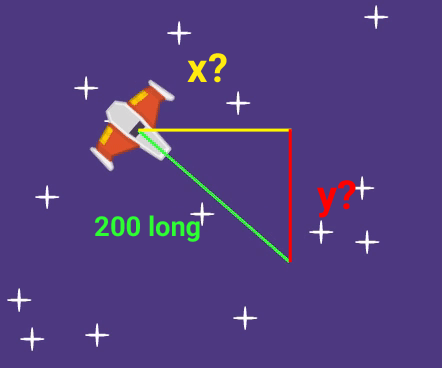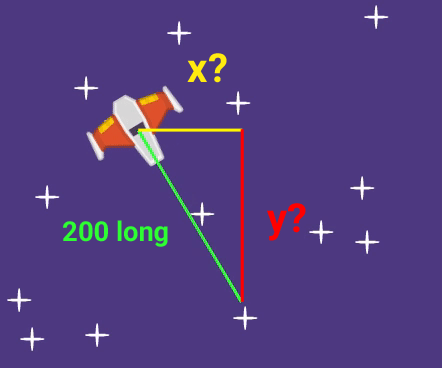
We can see that a triangle shape is formed if we look at the size of the x velocity (shown as a yellow line), the size of the y velocity (shown as a red line), and the size of the directional velocity (shown as a green line). But we don't know how big the x velocity should be, and we don't know how big the y velocity should be.

We'll start to get the blocks we need to determine the x and y velocity. For our directional velocity, grab a number block (0 from Operators), drag it into the script workspace, and type 200 into it. Make sure you also have the "Set velocity x" and "Set velocity y" blocks as well.

Luckily we do know one other piece of valuable information, and that's the angle that the ship has rotated.

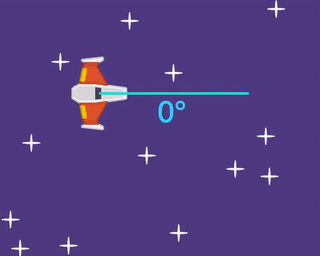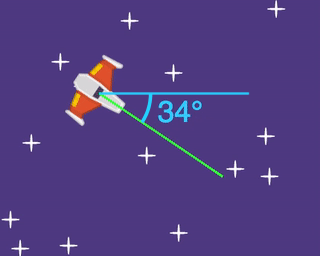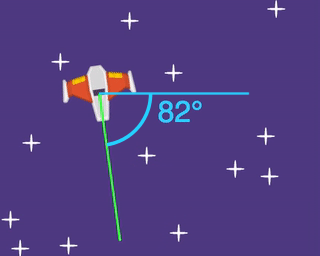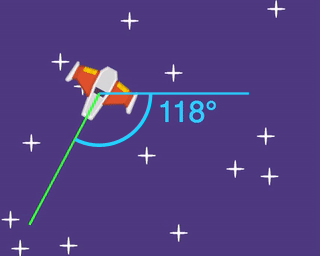
The angle is the same as the rotation, so grab the "rotation of myself" block (from Transform) and add it to our group of blocks.

Sin and Cos

Fortunately there is a whole branch of mathematics called trigonometry that's devoted to figuring out information about triangles! (If you'd like to learn more you can check out this page: http://math2.org/math/algebra/functions/sincos/)

We'll use two equations that use Sine (sin) and Cosine (cos). They'll let us figure out how big the x and y velocities should be, as long as we know what the angle of the triangle is, and what the length of one side of the triangle is.

sin Angle = Opposite/Hypotenuse

cos Angle = Adjacent/Hypotenuse

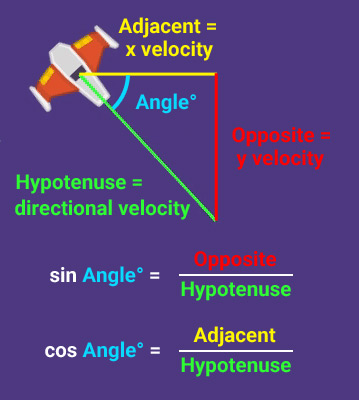
In our game, the Angle is the player's rotation, the hypotenuse of the triangle is our directional velocity (which = 200), the opposite side of the triangle is the y velocity, and the adjacent side of the triangle is the x velocity. We can make those equations even clearer:

sin Rotation = y velocity/directional velocity

cos Rotation = x velocity/directional velocity

Here's an example that shows how the math works:

Since we know the directional velocity is 200, we can shuffle the above equations to isolate the x velocity and y velocity like this:

sin Rotation = y velocity/200

200 × sin Rotation = y velocity

and

cos Rotation = x velocity/200

200 × cos Rotation = x velocity

Since sin and cos are the last pieces of the equation we need, grab the sin and cos blocks (both from Operators) and add them to our group of blocks.

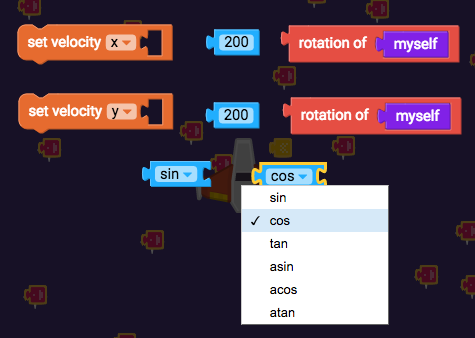
We now know that 200 × cos Rotation = x velocity, so grab a "×" block from Operators, and drag it into the "set x velocity" block. Then put "200" in the left side of it, and join "cos" with "rotation of myself", and put those in the right side.

We also know that 200 × sin Rotation = y velocity, so grab the same blocks except with "set velocity y" and "sin".

We want to set these velocities when the player is told to move forwards, so drag them into "if true/false forwards = true".

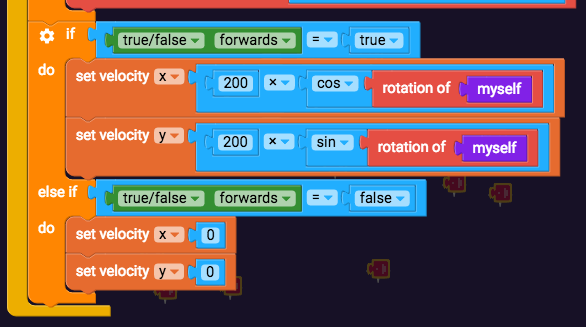
Now play your game to see if moving forwards works properly.

The rotation is almost right, but this ship flies towards the right instead of straight ahead.