Introduction to Inverse Tangents

In this chapter, we'll make our monkey aim in different directions. We'll use tangents to get the angles.

Before we begin, be warned: this chapter uses a simple method which sometimes gets the wrong answers. In the next chapter, we'll fix the bug. Don't panic.

Key Terminology

Before we go on, you should understand the following terms. You don't need to know everything about them, but you need to recognize them.

• Right-angle triangle
• Adjacent, opposite, hypotenuse sides
• Radius
• Origin (of a circle or vector)
• Vector
• Vector components (X and Y)
• Sine, cosine, and tangent

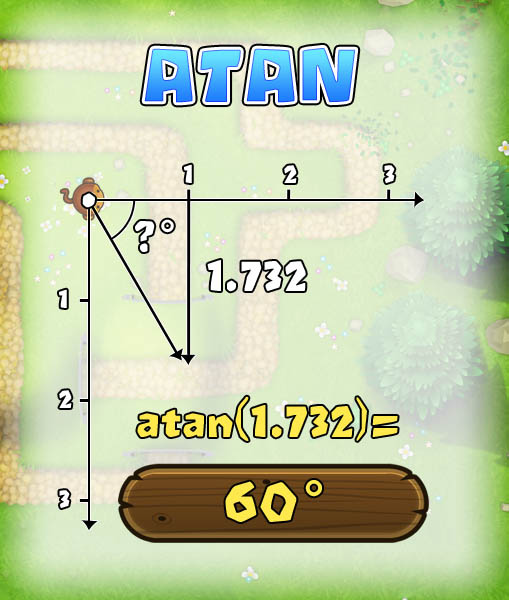
Inverse Tangent or atan

The atan operation lets us get an angle. How does that work? Let's find out - and then use it in our game.

Tangent, or tan, gives us the length of the opposite side in a right-angle triangle where the adjacent side is 1 and we know the angle. We will write it like this:

Y = tan( angle )

The inverse tangent, or atan, reverses this operation. It gives us the angle of a right-angle triangle where the adjacent side is 1 and we know the opposite side. We will write it like this:

angle = atan( Y )

Finding Vector Directions with atan

Here's where atan gets really useful. If we know the X and Y components of a vector, we can use atan to get the angle of that vector.

In our previous examples, we have assumed that the adjacent (X) side of the triangle is 1. But our vector might have a different X.

(X, Y) = (3, 2)

We can resize our vector by dividing both components by the same number. If we divide by X, we simplify the vector.

(X/X, Y/X) = (2/2, 2/3)

(1, Y/X) = (1, 0.66...)

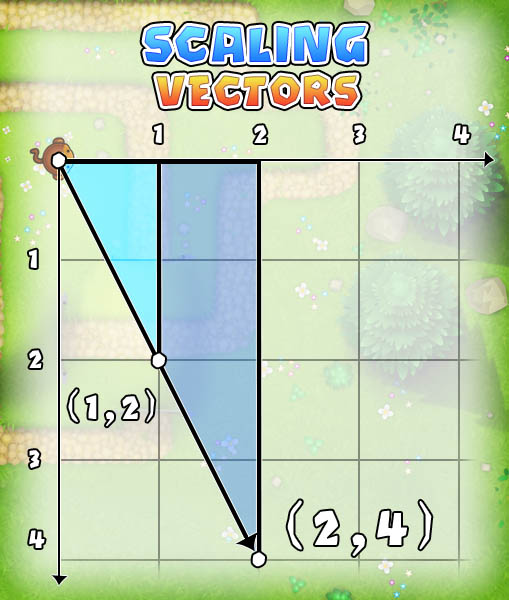
See that we've just changed the size of the vector, not its direction.

If we replace (Y, X) with (Y/X, 1), we can use atan to calculate the angle of any sized vector.

angle = atan( Y/X )

so for (3, 2)

angle = atan( 2/3 )

angle = 33.69 degrees

With this knowledge, we can measure the angle to anything where we know the X and Y coordinates.

Applying atan

Let's put atan to work in our game.

Play the game. If you performed the earlier steps correctly, you can press the game, and your monkey will fire to the right. We're going to get it to fire at the place you pressed!

Open up the Tower Controller script again.

Locate the function called to attack with: monkey.

Remember that your monkey fired to the right. Why was this?

It's because we initialized angle to be 0, and 0 degrees points to the right. If we want to change the direction your monkey fires, we'll have to set angle to some other value.

First, we're going to get a vector from the monkey to the target.

Subtract the X and Y coordinates of the monkey from the X and Y coordinates of the target. The target is stored in the properties targetX and targetY.

• Set dx to targetX - x position of monkey.
• Set dy to targetY - y position of monkey.

Now we know the X and Y components of the vector, we have everything we need to compute the angle of that vector. If we aim down that angle, we will be aiming at the target!

• Set angle to atan dy / dx.
• Play your game.

If you have performed the steps correctly, you will see your monkey now shoots at an angle when you press.

But what's this? Sometimes it's not the proper angle! If you click in all four corners of the game, you'll see your monkey sometimes shoots in the opposite direction. This happens when you click to the left of the monkey. Under some circumstances, you might even get an error message.

This is an expected bug. In the next section, we'll discover why it happens, and how to fix it.

For now, you've got a monkey that changes aim depending on where you click.