Measuring Distance with Pythagoras

Another common task in computer games is measuring distance. We must know if two objects are close together or far apart. For example, we might be keen to know if a thief just bumped into a china cabinet, or if the guard is too far away to hear the ensuing clatter.

Good news. It's very easy to measure distance, using the very same vectors we used with atan. All you need is the Pythagorean Theorem.

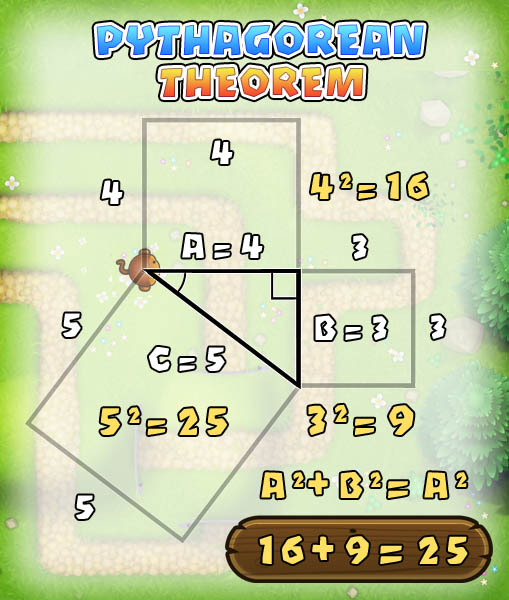
The Theorem states that the square of the hypotenuse in a right-angle triangle is equal to the square of the other two sides, or more succinctly:

A^2 + B^2 = C^2

We're not interested in knowing squares, so we can rearrange:

C = sqrt( A^2 + B^2 )

And that's the version we'll use to find the hypotenuse.

Measuring Distance Between Two Points

We can use Pythagoras to measure distances. In fact, this is how we measure the length of a vector. Once we have constructed a vector, we can use the X and Y components of that vector as sides A and B of a right-angle triangle. Thus the hypotenuse or length is the square root of A^2 + B^2.

This is going to come in super handy.